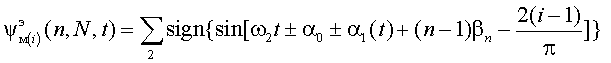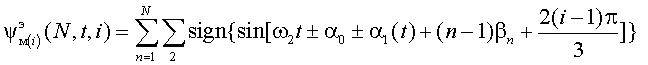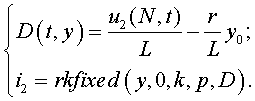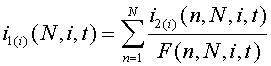|
|||
| Главная | Справочник | Схемотека | Нормативы | Форум | Статьи | Выставки | Пресс-релизы | | |||
| Главная >> Обзоры. Статьи. Информация. >> Электротехника. >> Математическая модель преобразователей частоты. | ||||||||||
Математическая модель преобразователей частоты. |
||||||||||
|
При описании процессов формирования выходных квазисинусоидальных напряжений (КСН) преобразователей частоты (ПЧ) их мгновенные значения чаще всего представляются в виде тригонометрического ряда Фурье с бесконечным числом гармонических составляющих. Такой подход дает положительные результаты при анализе гармонического состава и интегральных характеристик КСН, однако малоэффективен при их синтезе. В работе представляются результаты исследований по созданию математической модели ПЧ, отображающей как формирование выходных КСН и токов нагрузки, так и процессы формирования потребляемых токов из первичных систем электропитания без применения разложения в ряд Фурье. Представление результатов проводится на примере создания математической модели преобразователей частоты с квазиоднополосной модуляцией (ПЧ с КМ) [1]. В ПЧ с КМ реализуется многоканальный способ преобразования параметров электромагнитной энергии сети, при котором в блоке силовых модуляторов осуществляется разветвленная пофазная модуляция напряжений ui частоты w1 трехфазной сети соответствующими им эквивалентными модулирующими воздействиями yЭM(i)(N,t,i) трехфазной системы частоты w2. Математическая модель включает многопараметрическое алгоритмическое уравнение, описывающее процессы формирования выходных напряжений u2(N,t) ПЧ с КМ:
где Для силового модулятора напряжения любой из фаз, состоящего из N инверторов, эквивалентное модулирующее воздействие любого n-ного из них представим модулирующей функцией вида:
где a0 – половина временного интервала длительности нулевой паузы в кривой выходного напряжения n-ного инвертора; bn – начальная фаза выходного напряжения n-ного инвертора; a1(t)– угол управления, изменение которого во времени обеспечивает ШИР выходного напряжения каждого из инверторов и тем самым регулирование выходного напряжения ПЧ с КМ. Учитывая структурную организацию ПЧ с КМ, подключенного к трехфазной сети, эквивалентное модулирующее воздействие любого из трех силовых модуляторов:
Подставляя (3) в (1), получим математическую модель процесса формирования выходных КСН ПЧ с КМ при любом количестве инверторов, входящих в состав силовых модуляторов. Записывая алгоритмическое уравнение (1) относительно конкретного фазного напряжение с учетом (2), несложно получить любой промежуточный результат многоступенчатого процесса формирования КСН. При соответствующей нормировке (3) относительно питающего напряжения может быть использовано в качестве математической модели при описании электромагнитных процессов в двухзвенных преобразователях частоты, как с трехфазным, так и с однофазными выходным напряжением. Ток i2 RL-нагруки ПЧ с КМ определяется из решения дифференциального уравнения:
Такой же результат получим, при использовании для записи тока i2 метода наложения, предварительно определив составляющие его с учетом составляющих напряжения u2(N,t). Второй подход представления тока i2 удобен при определении математической модели формирования потребляемых фазных токов i1(i), которая отображается выражением:
где F(n,N,i,t) – функция преобразования для n-ного инвертора i-той фазы силовых модуляторов, совпадающая по виду с (2) при соответствующих параметрах n, N, i. ЛИТЕРАТУРА
|
|
| |
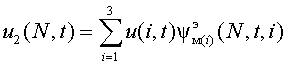
 – мгновенные значения фазных напряжений сети; Em
– амплитудное значение фазного напряжения, i = 1, 2,
3; N – число инверторов переменного напряжения силового
модулятора напряжения сети i-той фазы.
– мгновенные значения фазных напряжений сети; Em
– амплитудное значение фазного напряжения, i = 1, 2,
3; N – число инверторов переменного напряжения силового
модулятора напряжения сети i-той фазы.