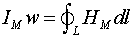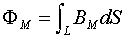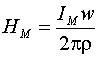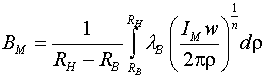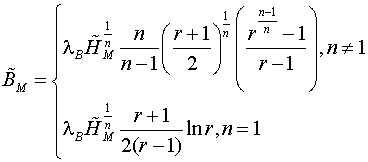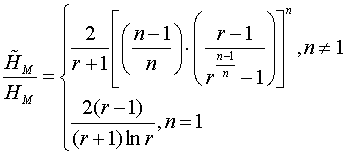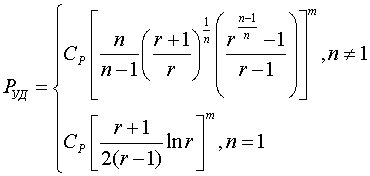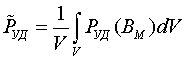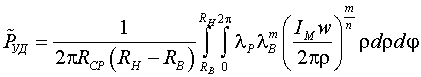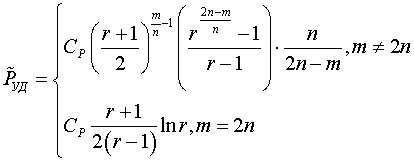|
|||
| Главная | Справочник | Схемотека | Нормативы | Форум | Статьи | Выставки | Пресс-релизы | | |||
| Главная >> Обзоры. Статьи. Информация. >> Электротехника. >> Измерение магнитных характеристик листовых электротехнических сталей на кольцевых образцах. | ||||||||||||||||||||||||||||||||||
Измерение магнитных характеристик листовых электротехнических сталей на кольцевых образцах. |
||||||||||||||||||||||||||||||||||
|
Для измерения магнитных характеристик холоднокатанных листовых электротехнических сталей (ЛЭС) используются в основном смешанные полосовые образцы (ПО) размером 280х30 мм, набираемые из полос вдоль и поперек направления прокатки (НП) и намагничиваемые в аппарате Эпштейна [3]. Однако специальные исследования и опыт применения [4, 5] показывают, что для электрических машин, являющихся основным потребителем динамных ЛЭС, лучшую сходимость с экспериментом при проектировании и расчетах дает использование эквивалентных магнитных характеристик, снимаемых на штампованных кольцевых образцах (КО) [3]. Следует отметить, что благодаря симметрии формы, отсутствию угловых зон, создание более однородного магнитного поля (МП) при намагничивании, КО обладают более высокими по сравнению с ПО метрологическими свойствами. Условия перемагничивания КО наиболее соответствуют режимам перемагничивания электрических машин. Однако, многие энергомашиностроительные предприятия получают ЛЭС в виде ленты шириной менее 280 мм, что не позволяет производить входной контроль магнитных свойств на стандартных ПО. Решение этой проблемы также возможно с использованием КО. Одним из существенных факторов, сдерживающих внедрение КО, является отсутствие обоснованных рекомендаций на размеры, выработка которых невозможна без исследования методической погрешности измерений (МПИ). Появление МПИ обуславливается неоднородностью МП образца в зоне расположения измерительных датчиков, связанной с совокупным действием целого ряда факторов. При этом наиболее существенное влияние могут оказывать: способы намагничивания и измерения магнитных характеристик; соотношение геометрических размеров намагничивающей зоны образца; нелинейность и анизотропия магнитных свойств (АМС) стали; различного рода внутренние механические напряжения в материале образца. В связи с совместным влиянием на МПИ магнитных характеристик значительного числа факторов и трудностью на практике выделения степени и характера влияния отдельных факторов наиболее эффективным методам анализа магнитных характеристик, определяемых на кольцевых образцах, является математическое моделирование их магнитного поля в зоне намагничивания. Универсальность такого подхода обеспечивается за счет возможности проведения широкого исследования на одной модели и в частности оценки влияния на МПИ магнитных характеристик каждого из исследуемых факторов независимо друг от друга [2]. При моделировании МП исходим из того, что НП отдельных пластин (жестей) в образце совпадают. Полагаем также на основании результатов теоретических исследований, что гистерезисным характером кривых намагничивания материала при расчете МП можно пренебречь. С учетом принятых допущений рассматриваемую задачу, решаем на основе математической модели плоского статического МП кольцевого шихтованного сердечника (ШС). При этом основной целью задачи является определение степени различия между истинными характеристиками материала и измеряемыми удельными характеристиками образца. При измерении эквивалентных магнитных характеристик ЛЭС на КО в
соответствии с ГОСТ [3] намагничивается весь образец, причем намагничивающая
и измерительная обмотки наносятся непосредственно на образец. Под
эквивалентными характеристиками исследуемой стали при заданной частоте
перемагничивания понимаются характеристики испытуемого образца
Неравномерность распределения МП по ширине спинки КО даже при отсутствии
АМС приводит к различию измеренных на нем эквивалентных магнитных
характеристик с аналогичными характеристиками стальной пластины
BM(HM)
и PУД(BМ),
где BM, HM
и PУД - амплитудные значения векторов
МП и удельные магнитные потери в локальной области листовой стали,
для которой МП можно принять однородным. В связи с неизменностью
магнитного потока в образце независимо от характера распределения
МП по его сечению всегда принимается, что
При отсутствии АМС и аппроксимации магнитных характеристик материала степенными функциями вида y = x1/n и y = xn, удается получить удобные для последующего анализа dН и dР аналитические выражения [2].
где lВ и lР - масштабные коэффициенты; n и m - показатели нелинейности соответствующих магнитных характеристик, зависящие от величины BМ. Применительно к КО такая постановка задачи представляет интерес в связи с наличием у определенной группы ЛЭС весьма слабо выраженной АМС. В теоретическом плане появляется также возможность выделить отдельно влияние на МПИ соотношения размеров КО и нелинейности магнитных свойств материала.
Области значения и характер изменения n(BМ)
и m(BМ) для холоднокатанных
ЛЭС представлены на рис. 1 заштрихованными зонами (величины n
и m определялись для бесконечно малых участков магнитных
характеристик материала). Известно, что при перемагничивании изотропного
КО имеет место изменение амплитудного значения индукции по ширине
спинки. Однако, из рис. 1 следует, что в ненасыщенных режимах намагничивания,
когда неоднородность МП максимальна, изменение n происходит
в достаточно узких пределах, а величина m остается постоянной
и равна 1,8-1,9. С ростом насыщения изменение n и m
от BМ становится значительным, но при
этом резко снижается перераспределение МП по ширине спинки [1].
Поэтому приемлемо допущение, что показатели n и m
в пределах изменения BМ по ширине спинки
КО остаются неизменными и равными n(BМ)
и m(BМ). Полагаем также,
что несинусоидальность мгновенных значений B(t)
при насыщении не оказывает влияния на характер зависимости PУД(BМ)
в различных точках по ширине спинки КО. Рассмотрим МП кольцевого ферромагнитного сердечника. Из уравнений МП для квазистатики представим связь между амплитудными магнитными характеристиками сердечника и материала:
где L - произвольный связанный со всеми витками намагничивающей обмотки замкнутый контур интегрирования. Учитывая при интегрировании (8), что МП является плоским, а поток не вытесняется из магнитопровода, получаем известное выражение для напряженности МП HМ в произвольной точке сердечника с радиальной координатой r:
тогда из (1) и (9) имеем:
В результате устанавливаем характер зависимости между
Подставляя (12) в (6), получаем зависимость величин, входящих в выражение (4) для:
Внешний вид (13) указывает, что погрешность dН зависит только от соотношения радиусов КО r и степени нелинейности кривой намагничивания, связанной с коэффициентом n. Поскольку удельные магнитные потери в КО ставятся в соответствие
величине
Удельные магнитные потери в сердечнике
или для решаемой плоской задачи с учетом (7), (11):
После интегрирования (16) получаем выражение для
Из (14), (17) следует, что вид выражения для d, определяемого подстановкой последних в (5) будет зависеть как от n, так и от соотношения n и m. Сама МПИ является функцией безразмерных параметров: m, n, r. 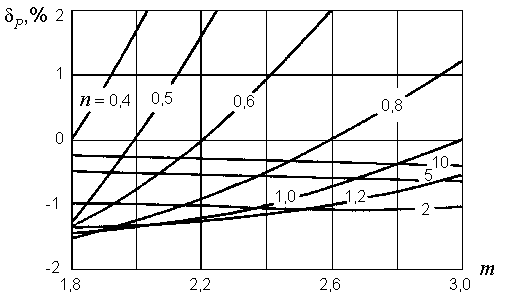
Рис. 2. Расчетные зависимости dP(m) ЛЭС при различных n = const и r = 1,4. Проведенные исследования показывают, что погрешность dP при r = const и n > 2 практически не зависит от m (Рис. 2). Следовательно, если учесть, что для ЛЭС при n Ј 2 m » 1,85 (Рис. 1) и не зависит от n, а при n і 2 не зависит от m, dP всегда можно вычислять при m = 1,85. Соотношения n и m ЛЭС на рис. 1, позволяют утверждать, что погрешности dН и dP всегда принимают отрицательные значения (иначе: свойства образца всегда лучше свойств материала, из которого он изготовлен). При оценке погрешности dP допущение о неизменности зависимости PУД(BМ) может быть снято, поскольку при слабом насыщении, при котором значения погрешности наибольшие, искажения формы магнитной индукции не происходит, а при значительном насыщении, приводящем к искажению формы B(t) погрешность dP асимптотически стремится к нулю. |
|
| |
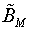 (
(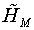 ) являются
) являются 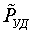 (
(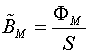
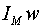 ;
;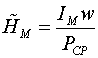
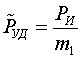
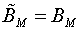 . Тогда возникающие при измерении МПИ напряженности МП и удельных
магнитных потерь соответствуют равенствам:
. Тогда возникающие при измерении МПИ напряженности МП и удельных
магнитных потерь соответствуют равенствам: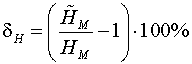
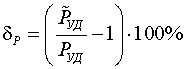
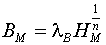
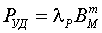
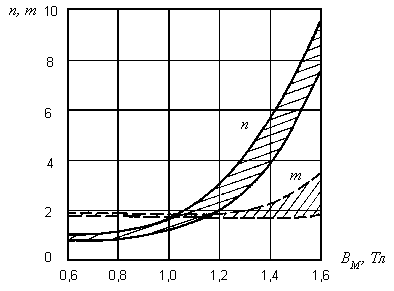 Рис. 1. Области значений n(BМ)
и m(BМ) холоднокатаных
ЛЭС.
Рис. 1. Области значений n(BМ)
и m(BМ) холоднокатаных
ЛЭС.